Identifying and Mitigating Instability in Embeddings of the Degenerate Core

• [Paper]
• [Supplemental Materials]

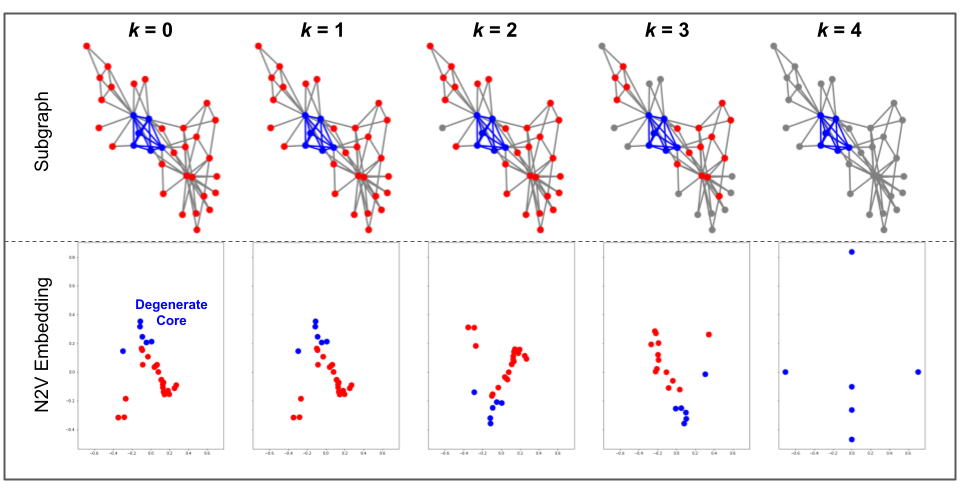
We measure stability of node embeddings by iteratively shaving off k-shells and re-embedding the graph. Instability is defined as perturbations to the embeddings of the degenerate core (k-core with maximum k) as the periphery is removed. The above example uses the Zachary Karate Club network and the Node2Vec embedding algorithm.

Abstract: Are the embeddings of a graph's degenerate core stable? What happens to the embeddings of nodes in the degenerate core as we systematically remove periphery nodes (by repeatedly peeling off k-cores)? We discover three patterns w.r.t. instability in degenerate-core embeddings across a variety of popular graph embedding algorithms and datasets. We correlate instability with an increase in edge density, and then theoretically show that in the case of Erdős–Rényi model graphs embedded with Laplacian Eigenmaps, the best and worst possible embeddings become less distinguishable as density increases. Furthermore, we present the STABLE algorithm, which takes an existing graph embedding algorithm and makes it stable. We show the effectiveness of STABLE in terms of making the degenerate-core embedding stable and still producing state-of-the-art link prediction performance.